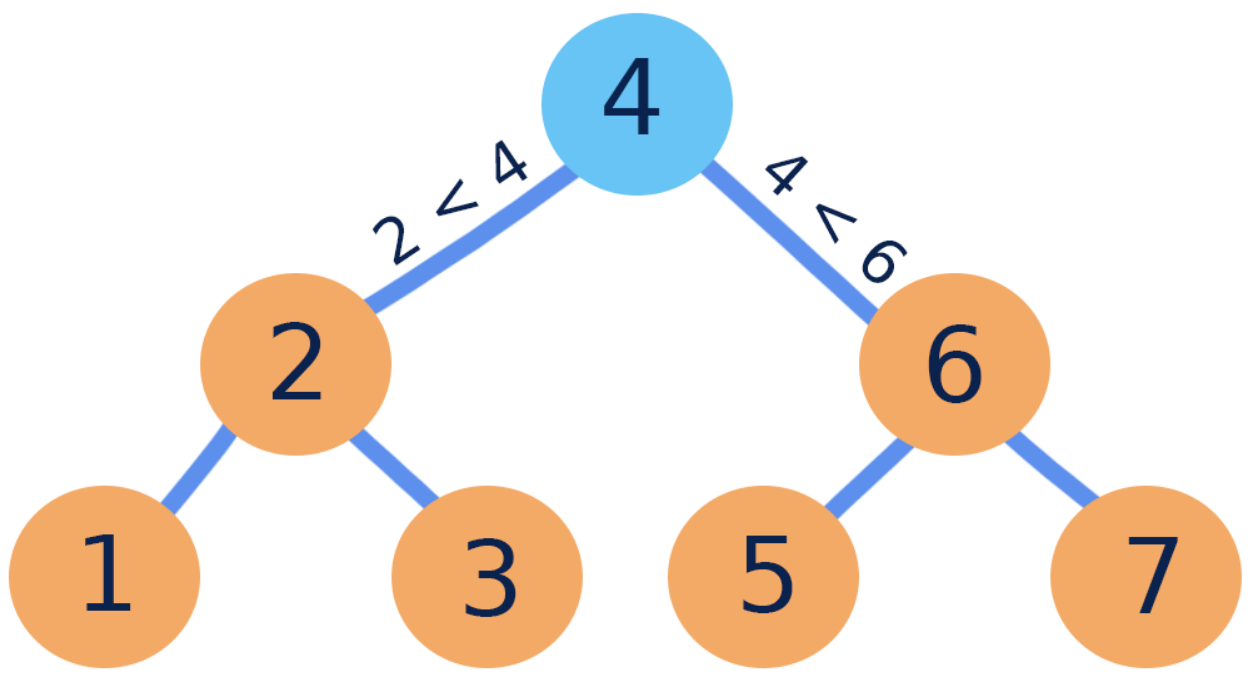
Understand Binary Search Trees (BST)

•By Abdellah Allali • 6 min read
Understand Binary Search Trees (BST)

What is a BST?

Definition

A Binary Search Tree (BST) is a hierarchical data structure in which each node has at most two children. The tree is organized such that:

  • Nodes in the left subtree contain values less than the parent node’s value.
  • Nodes in the right subtree contain values greater than the parent node’s value. This arrangement makes BSTs incredibly efficient for operations like searching, insertion, and deletion.

Real-World Analogy

ℹ️ Info

Imagine a dictionary where words are stored in alphabetical order. This allows you to quickly search for any word by leveraging the order to skip over large portions of irrelevant data. A Binary Search Tree (BST) follows a similar concept, where elements are arranged in a manner that allows efficient searching, insertion, and deletion.

Structure

A BST is a binary tree in which each node has at most two children, satisfying the following properties:

  1. The left subtree of a node contains only nodes with values less than the node’s value.
  2. The right subtree of a node contains only nodes with values greater than the node’s value.
  3. Both the left and right subtrees must themselves be BSTs.

Properties

💡 Tip

Key Characteristics:

  • Sorted Order: In-order traversal of a BST produces elements in ascending order.
  • Efficiency: Searching, insertion, and deletion have a time complexity of O(h), where h is the height of the tree.
  • Dynamic Growth: BSTs dynamically adjust their size as elements are inserted or deleted.

Searching

Algorithm

ℹ️ Info
  1. Start from the root node.
  2. Compare the target value with the current node’s value:
    • If equal, return the node.
    • If less, move to the left child.
    • If greater, move to the right child.
  3. Repeat until the target is found or the subtree is empty.

Illustration

For a tree with root 7 and target 9:

          7
           \
            12
            /
           9
  1. Start at 7. 9 > 7, move to the right.
  2. At 12, 9 < 12, move to the left.
  3. At 9, target is found.

Code Snapshot

BST_NODE *bst_find(int target, BST_NODE *head_node)
{
    if (head_node == NULL) return NULL;
    if (head_node->value < target)
        return bst_find(target, head_node->right);
    if (head_node->value > target)
        return bst_find(target, head_node->left);
    return head_node;
}

Insertion

Algorithm

ℹ️ Info
  1. Start at the root.
  2. Compare the value to be inserted with the current node’s value:
    • If less, move to the left child.
    • If greater, move to the right child.
  3. If the correct position is found (NULL child), insert the new node.

Illustration

Inserting 10 into this tree:

          7
        /   \
       5     12
            /
           9
  1. Start at 7. 10 > 7, move to the right.
  2. At 12, 10 < 12, move to the left.
  3. At 9, 10 > 9, insert as the right child of 9:
          7
        /   \
       5     12
            /
           9
             \
             10

Code Snapshot

bool bst_insert_node(BST_NODE **node_ptr, int value)
{
    if (*(node_ptr) == NULL)
    {
        *node_ptr = bst_create_tree(value);
        return true;
    }
    if (value > (*node_ptr)->value)
        return bst_insert_node(&(*node_ptr)->right, value);
    if (value < (*node_ptr)->value)
        return bst_insert_node(&(*(node_ptr))->left, value);
    return true;
}

Deletion

Algorithm

ℹ️ Info
  1. Locate the node to delete.
  2. Handle three cases:
    • No children: Remove the node directly.
    • One child: Replace the node with its child.
    • Two children: Replace the node with its in-order predecessor or successor.

Illustration

Deleting 12 from this tree:

          7
        /   \
       5     12
            /  \
           9    15
  1. Find 12. It has two children.
  2. Replace 12 with its in-order predecessor (9):
          7
        /   \
       5      9
               \
                15

Code Snapshot

BST_NODE *bst_delete_node(BST_NODE **root, int target)
{
    if (*root == NULL) return *root;
    if ((*root)->value < target)
        return bst_delete_node(&(*root)->right, target);
    else if ((*root)->value > target)
        return bst_delete_node(&(*root)->left, target);
    else
    {
        if ((*root)->right == NULL && (*root)->left == NULL)
        {
            free(*root);
            *root = NULL;
        }
        else if ((*root)->left == NULL)
        {
            BST_NODE *tmp = *root;
            *root = (*root)->right;
            free(tmp);
        }
        else if ((*root)->right == NULL)
        {
            BST_NODE *tmp = *root;
            *root = (*root)->left;
            free(tmp);
        }
        else
        {
            BST_NODE *proc = NULL;
            BST_NODE *suc = NULL;
            bst_find_predecessor_successor(*root, target, &proc, &suc);
            (*root)->value = proc->value;
            bst_delete_node(&(*root)->left, proc->value);
        }
    }
    return *root;
}

Traversals

In-Order Traversal

ℹ️ Info
  1. Visit the left subtree.
  2. Visit the current node.
  3. Visit the right subtree.

Illustration

For the tree:

          7
        /   \
       5     12
      / \    /
     3   6  9

The traversal sequence is: 3, 5, 6, 7, 9, 12.

Code Snapshot

void bst_in_order_traversal(BST_NODE *node, void (*callback)(BST_NODE *node))
{
    if (node == NULL) return;
    bst_in_order_traversal(node->left, callback);
    callback(node);
    bst_in_order_traversal(node->right, callback);
}

Level-Order Traversal

ℹ️ Info
  1. Use a queue to track nodes at each level.
  2. Enqueue the root.
  3. While the queue is not empty:
    • Dequeue a node.
    • Process it.
    • Enqueue its children (left, then right).

Illustration

For the same tree:

          7
        /   \
       5     12
      / \    /
     3   6  9

The traversal sequence is: 7, 5, 12, 3, 6, 9.

Code Snapshot

void bst_lvl_order_traverse_queue(BST_NODE *node, void (*callback)(BST_NODE *node))
{
    Queue *q = create_queue();
    enqueue(q, node);
    while (!queue_is_empty(q))
    {
        BST_NODE *current = (BST_NODE *)dequeue(q);
        callback(current);
        if (current->left != NULL) enqueue(q, current->left);
        if (current->right != NULL) enqueue(q, current->right);
    }
    free(q);
}

Examples with Code

Here’s an example tree built from a sequence of insertions:

          7
        /   \
       5     12
      / \    /  \
     3   6   9   15
    / \     / \    \
   1   4   8  10   17

Using the provided code, you can create and manipulate this tree:

BST_NODE *node = NULL;
node = bst_create_tree(7);
int values[] = {5, 12, 3, 6, 9, 15, 1, 4, 8, 10, 17};
for (int i = 0; i < sizeof(values)/sizeof(int); i++)
    bst_insert_node(&node, values[i]);
bst_print_tree(node);

Practical Use Cases

💡 Tip
  • Databases: Used in indexing and searching.
  • Compilers: Abstract syntax trees for parsing.
  • Networking: Efficient routing table lookups.